문제
* 피보나치 수열에서 N번째 숫자를 출력하는 문제
* 여기서 핵심은 순서가 최대 1000000000000000000번째까지라는 점이다.
* 또한, 출력은 1000000007로 나눈 나머지를 출력한다. 즉, 출력하는 숫자 자체는 int범위 안에서 해결가능
원리
결론적으로 말하자면 이 문제는 행렬 (선형대수) 푸는 것이 출제자의 의도다.
(필자는 피보나치를 보자마자 DP라고 생각했다가 헤맸다.)
여러개의 방정식을 하나의 핼렬꼴로 표현하면, 다음이 가능해진다.
1. 선형방정식의 해가 존재하는지 없는지 판단
2. 가우스 소거, 크래머 공식 등 여러 방법에 의해 쉽게 미지수에 대한 답 혹은 일반항을 찾기
즉, 다음과 같이 선형방정식을 행렬 꼴로 변환해서 풀이한다.
Ax = b 형태이에 관해 Stargazer_Lab님의 레퍼런스를 인용하자면 아래와 같다. (이해가 필요한 경우 열어보기)
1. Ax = b의 방정식을 행렬로 표현
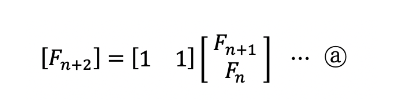
2. 여기에서 x가 나타내는 식을 추가해서 x를 공통인수로하는 하나의 선형방정식을 얻는다.
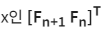
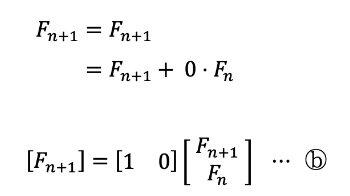
3. a식과 b식을 결합한다.
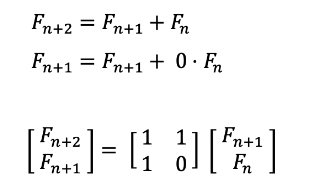
4. 3번의 식을 일반화하여, 다음과 같이 행렬꼴로 표현해 열벡터로 치환한다.
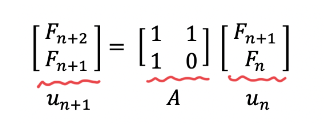
5. 이제 u벡터에 대해서, 피보나치 수열의 초기값을 대입해 u벡터의 초기값을 구한다.
(피보나치에서 1번째 = 0, 2번째 = 1임)
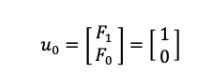
6. 이제 u1부터 위의 식에 대해 나열해본다.
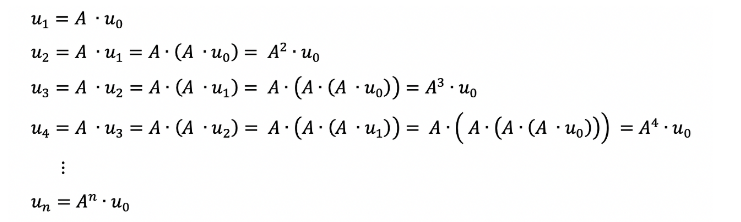
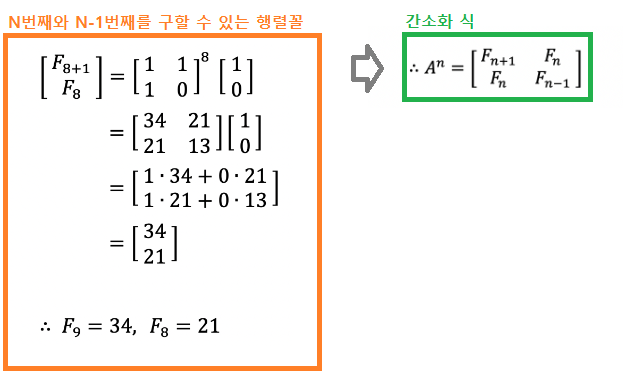
7. 결과적으로 A라는 행렬에 대한 n제곱이라는 식으로 피보나치 결과값을 구할 수 있다.
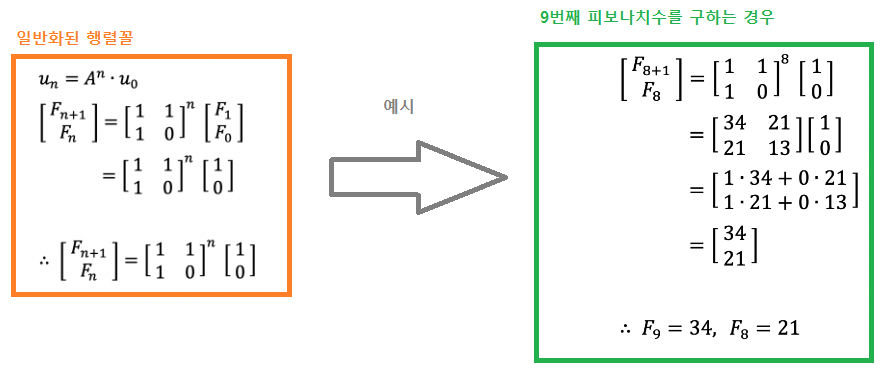
8. 이를 간소화 하면 다음과 같은 일반화 행렬식을 얻을 수 있다.
즉, 행렬 A인 ([1, 1], [1, 0]) 만 갖고도 행렬의 n제곱을 통해 피보나치 수를 얻을 수 있다.
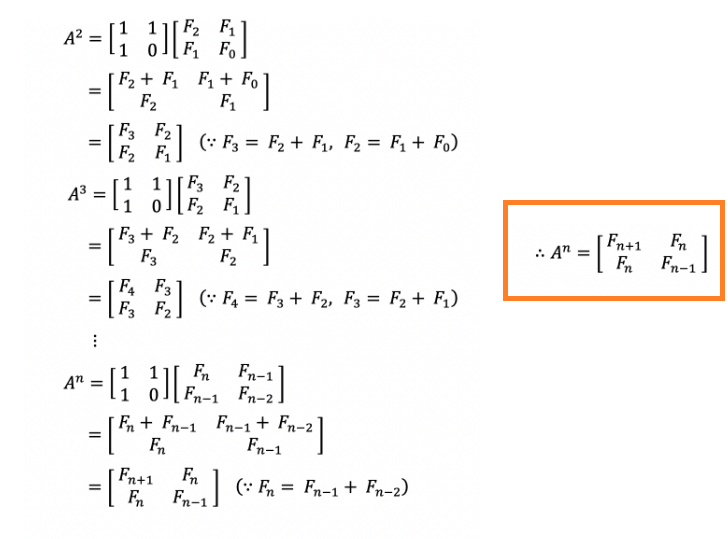
나의 코드
[실패] 시도1. 단순하게 DP라고 생각했다가 실패한 코드이다.
import java.io.*;
import java.math.BigInteger;
import java.util.ArrayList;
import java.util.List;
import java.util.StringTokenizer;
public class no11444 {
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static List<BigInteger> list = new ArrayList<>();
private static BigInteger mod = new BigInteger("1000000007");
public static void main(String[] args) throws IOException {
list.add(new BigInteger("0"));
list.add(new BigInteger("0"));
list.add(new BigInteger("1"));
int N = Integer.parseInt(br.readLine());
if(N==2) System.out.println(1);
else {
for(int i=3; i<=N ; i++) {
BigInteger two = list.get(i-2);
BigInteger one = list.get(i-1);
list.add(i, two.add(one));
}
System.out.println(list.get(N).mod(mod));
}
}
}
[성공] 시도2. 레퍼런스 이론과 코드를 바탕으로 Long대신 BigInteger를 이용해 풀이해보았다.
(사실상 이 문제에선 모듈러를 이용해 풀이하기때문에 Long 타입안에서 메모리가 해결이 된다.)
import java.io.*;
import java.math.BigInteger;
/**
* 재귀를 이용한 계산방식
*/
public class no11444 {
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static BigInteger mod = new BigInteger("1000000007");
private static BigInteger[][] base = {{new BigInteger("1"), new BigInteger("1")},
{new BigInteger("1"), new BigInteger("0")}};
public static void main(String[] args) throws Exception {
BigInteger N = new BigInteger(br.readLine());
/** 공식이 될 행렬
* |1 1| |F(n+1) F(n)|
* A^n = | | = | |
* |1 0| |F(n) F(n-1)|
*/
BigInteger[][] A = {{new BigInteger("1"), new BigInteger("1")},
{new BigInteger("1"), new BigInteger("0")}};
System.out.println(pow(A, N.subtract(new BigInteger("1")))[0][0]);
}
private static BigInteger[][] pow(BigInteger[][] A, BigInteger exp) {
if(exp.equals(new BigInteger("1")) || exp.equals(new BigInteger("0"))) return A; // 지수가 1 또는 O인 경우
BigInteger[][] ret = pow(A, exp.divide(new BigInteger("2"))); // 지수를 절반으로 분할하여 재귀 호출
ret = multiply(ret,ret);
if(exp.mod(new BigInteger("2")).equals(new BigInteger("1"))) ret = multiply(ret, base);
return ret;
}
private static BigInteger[][] multiply(BigInteger[][] o1, BigInteger[][] o2) {
BigInteger[][] ret = new BigInteger[2][2];
ret[0][0] = ((o1[0][0]).multiply(o2[0][0])).add((o1[0][1].multiply(o2[1][0]))).mod(mod);
ret[0][1] = ((o1[0][0]).multiply(o2[0][1])).add((o1[0][1].multiply(o2[1][1]))).mod(mod);
ret[1][0] = ((o1[1][0]).multiply(o2[0][0])).add((o1[1][1].multiply(o2[1][0]))).mod(mod);
ret[1][1] = ((o1[1][0]).multiply(o2[0][1])).add((o1[1][1].multiply(o2[1][1]))).mod(mod);
return ret;
}
}
레퍼런스 코드
참고링크 : https://st-lab.tistory.com/252
'알고리즘 저장소 (일반방식과 나만의 풀이) > JAVA' 카테고리의 다른 글
| [백준] no21736: 헌내기는 친구가 필요해 - BFS 지도탐색 (0) | 2023.06.07 |
|---|---|
| [백준] no14940: 쉬운 최단거리 (0) | 2023.06.06 |
| [백준] no10768: 특별한 날 (0) | 2023.06.04 |
| [백준] no1967: 트리의 지름 (0) | 2023.06.02 |
| [백준] no11404: 플로이드 - BFS + 우선순위큐 (0) | 2023.06.01 |

![[백준] no11444: 피보나치 수 6 - 수학(행렬)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fbkuyu8%2FbtsiyWMZ7az%2FFs4DntmIiee2acdKzTxXaK%2Fimg.jpg)