728x90
문제
Input
N : 행렬의 크기 (정사각 배열)
B : 행렬을 제곱할 횟수 (지수)
N x N의 행렬Output
최초 행렬을 B번 제곱한 행렬문제 링크 : https://www.acmicpc.net/problem/10830
원리
1. 분할정복
즉, B를 2로 꾸준히 나누어 가며, 나머지가 1인경우(지수가 홀수)와 나머지가 0인 경우(지수가 짝수)에 따라 행렬곱 연산
가령 지수 B가 5일 경우, 2제곱 * 2제곱 * 1제곱과 같다.
따라서, 2제곱인 경우는 한 번만 구하면 된다는 설정.
이는 다음 레퍼런스 그래프 설명으로 쉽게 이해할 수 있다. (출처 : https://st-lab.tistory.com/251)
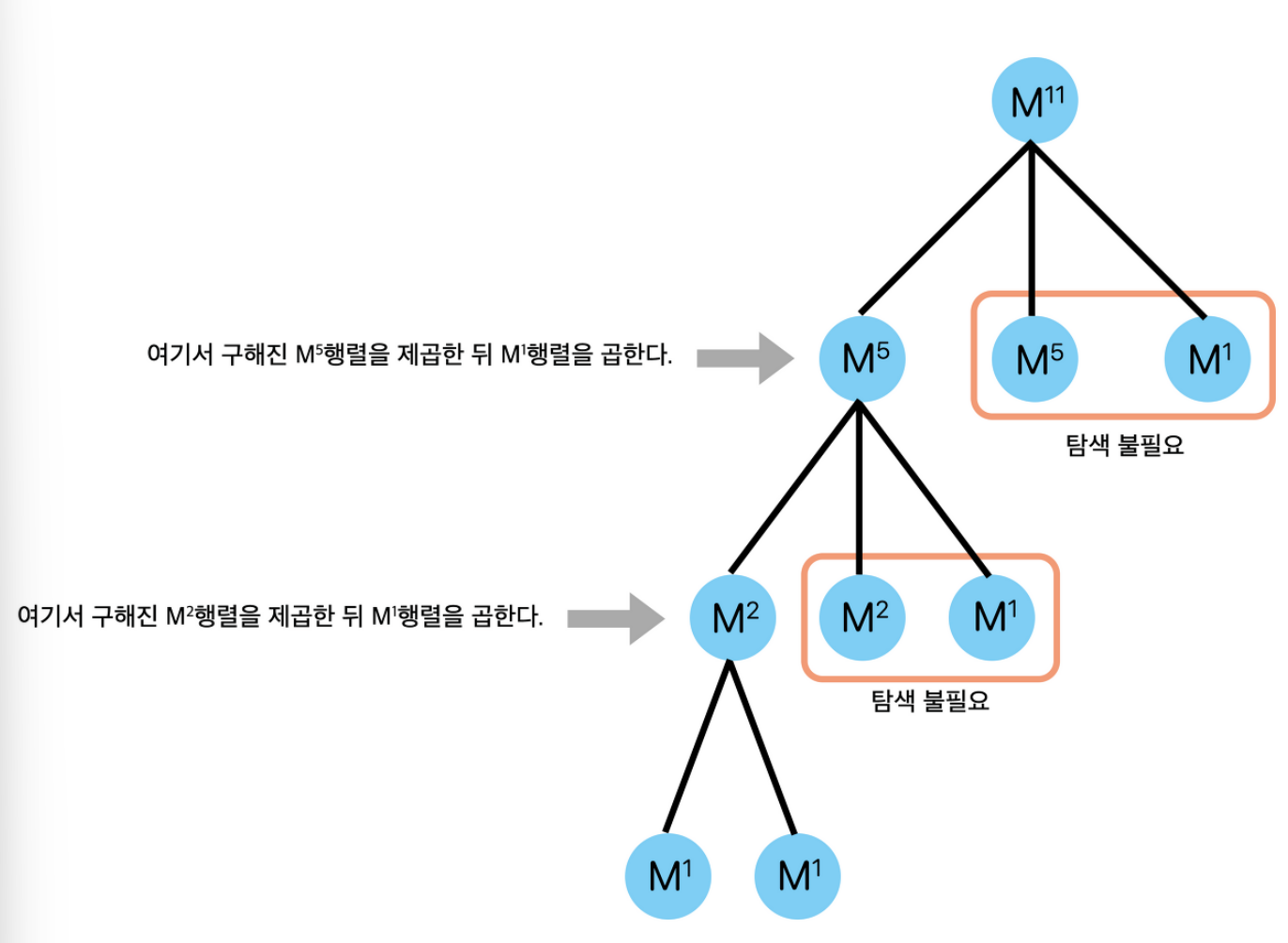
2. 행렬곱 코드
/**
* 두 행렬 mat1과 mat2에 대해 반복문을 이용한 기본 곱셈 공식
* N은 행렬의 길이이며, N*N 사이즈의 행렬에 대한 곱셈공식
* mod는 결과값이 메모리 초과가 발생하지 않도록 나누어주는 모듈러로서 여기선 1000을 사용했다.
*/
private static int[][] multifly(int[][] mat1, int[][] mat2) {
int [][] result = new int [N][N];
for(int i=0 ; i<N ; i++) {
for(int j=0 ; j<N ; j++) {
for(int k=0 ; k<N ; k++) {
result[i][j] += mat1[i][k] * mat2[k][j];
result[i][j] %= mod; // 연산이 끝날때마다 모듈러 연산
}
}
}
return result;
}나의 코드
처음 분할정복이라는 개념을 몰랐을 때, 단순히 수학적으로 생각했다.
반을 나눠 나누어 떨어지는 경우엔 같은 행렬을 곱하고, 1이 남는 경우는 거기에 최초 행렬을 더 곱해주는 방식.
따라서 주어진 B를 2로 나눈 경우 나머지가 1인경우와 0인 경우를 나눠 계산하기 위해 Stack을 생각했던 코드.
import java.io.*;
import java.util.Stack;
import java.util.StringTokenizer;
/**
* 분할 정복 : B를 나눠 불필요한 탐색을 최소화
*/
public class no10830 {
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
private static int N;
private static long B;
private static int[][] origin;
private static int mod = 1000;
private static Stack<Integer> stack = new Stack<>();
private static int[][] multi_matrix;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
// 입력 구간
N = Integer.parseInt(st.nextToken());
B = Long.parseLong(st.nextToken());
origin = new int[N][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < N; j++) origin[i][j] = Integer.parseInt(st.nextToken()) % mod;
}
// Stack에 저장한 순서대로 코드 호출
while (B != 1) {
if (B % 2 == 1) stack.push(1);
else stack.push(0);
B /= 2;
}
multi_matrix = origin;
while(!stack.isEmpty()) {
int now = stack.pop();
pow2(now);
}
for(int i=0 ; i<N ; i++) {
for(int j=0 ; j<N; j++) {
bw.append("" + multi_matrix[i][j]).append(" ");
}
bw.write("\n");
}
bw.close();
}
/**
* 경우에 따른 행렬 연산
*/
private static void pow2 (int now) {
if(now==0) {
multi_matrix = multifly(multi_matrix, multi_matrix);
} else {
multi_matrix = multifly(origin, multifly(multi_matrix, multi_matrix));
}
}
/**
* 행렬 * 행렬 메소드
* 1번 경우 : 재귀로 얻은 동일 행렬 (mat1 == mat2)
* 2번 경우 : 재귀로 얻은 행렬 * 초기행렬
*/
private static int[][] multifly(int[][] mat1, int[][] mat2) {
int [][] result = new int [N][N];
for(int i=0 ; i<N ; i++) {
for(int j=0 ; j<N ; j++) {
for(int k=0 ; k<N ; k++) {
result[i][j] += mat1[i][k] * mat2[k][j];
result[i][j] %= mod; // 연산이 끝날때마다 모듈러 연산
}
}
}
return result;
}
}레퍼런스
더보기
private static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
private static BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
private static int N;
private static long B;
private static int[][] origin;
private static int mod = 1000;
public static void main(String[] args) throws IOException {
StringTokenizer st = new StringTokenizer(br.readLine(), " ");
N = Integer.parseInt(st.nextToken());
B = Long.parseLong(st.nextToken());
origin = new int[N][N];
for (int i = 0; i < N; i++) {
st = new StringTokenizer(br.readLine(), " ");
for (int j = 0; j < N; j++) origin[i][j] = Integer.parseInt(st.nextToken()) % mod;
}
int[][] result = pow(origin, B);
for(int i=0 ; i<N ; i++) {
for(int j=0 ; j<N; j++) {
bw.append("" + result[i][j]).append(" ");
}
bw.write("\n");
}
bw.close();
}
/**
*
* @param matrix : 대상이 되는 행렬
* @param exp : 현재의 지수
* @return 반환될 행렬
*/
private static int[][] pow (int[][] matrix, long exp) {
// 지수가 1일 땐 A를 반환
if(exp == 1L) return matrix;
// 지수를 절반으로 분할하여 재귀
int[][] temp = pow(matrix, exp/2);
// 하위 재귀에서 얻은 행렬을 제곱
temp = multifly(temp, temp);
// 지수가 홀수 일 때,
if(exp % 2 == 1L) temp = multifly(temp, origin);
return temp;
}
/**
* 행렬 * 행렬 메소드
* 1번 경우 : 재귀로 얻은 동일 행렬 (mat1 == mat2)
* 2번 경우 : 재귀로 얻은 행렬 * 초기행렬
*/
private static int[][] multifly(int[][] mat1, int[][] mat2) {
int [][] result = new int [N][N];
for(int i=0 ; i<N ; i++) {
for(int j=0 ; j<N ; j++) {
for(int k=0 ; k<N ; k++) {
result[i][j] += mat1[i][k] * mat2[k][j];
result[i][j] %= mod; // 연산이 끝날때마다 모듈러 연산
}
}
}
return result;
}참고 링크 : https://st-lab.tistory.com/251
728x90
'알고리즘 저장소 (일반방식과 나만의 풀이) > JAVA' 카테고리의 다른 글
| [백준] no14938:서강그라운드 - 다익스트라(Dijkstra) (0) | 2023.07.22 |
|---|---|
| [백준] no2448: 별 찍기11 - 재귀 (0) | 2023.07.20 |
| [백준] no2096:내려가기 - 슬라이딩 윈도우 기법 DP (0) | 2023.06.28 |
| [백준] no1916: 최소비용 구하기 - 우선순위큐 다익스트라 (0) | 2023.06.26 |
| [백준] no1918: 후위 표기식 (0) | 2023.06.25 |

![[백준] no10830:행렬 제곱 - 분할정복](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdna%2FbSLGEw%2Fbtsn7NRYkqo%2FAAAAAAAAAAAAAAAAAAAAALpDe4zFUMrZpUTCMT4EWyhs-cLiIUO1SOK9kt781XsL%2Fimg.jpg%3Fcredential%3DyqXZFxpELC7KVnFOS48ylbz2pIh7yKj8%26expires%3D1772290799%26allow_ip%3D%26allow_referer%3D%26signature%3DJN%252BpSANTTQgB5GrVMPKfjHF6q%252Bk%253D)